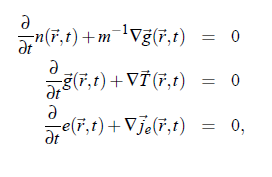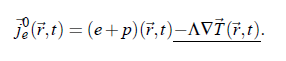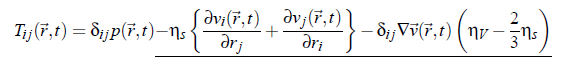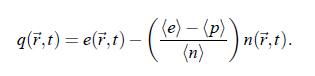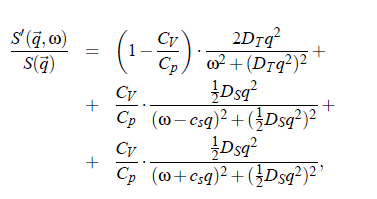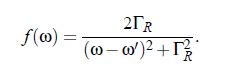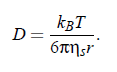2004-(II)-Dynamic light scattering
Article Index
Spectrum of scattered field - hydrodynamic considerations:
For the interpretation of the scattered spectrum of a fluid it is useful to consider the scattered field in terms of hydrodynamic approaches. In order to get access to hydrodynamics, the conservation and continuity equations have to be applied to a fluid volume element:
with the particle number density n(~r ,t ), the vector of momentum density g~(~r ,t ), the m mass, as well as the energy density e(~r ,t ). T (~r ,t ) is the stress tensor and j e (~r ,t ) the energy flux density. Finally, the expression of energy flux density is given by:
However, in the general case when the viscosity of fluid is not neglected, the expression of momentum density has to be completed to account for the volume viscosity ηV and the shear viscosity η. Consequently:
follows. In conclusion, with the aid of the equations of conservation and continuity a complete mathematical mean-field description of the hydrodynamics of a liquid results. The evaluation of the relations necessitates a linearization of the coupled differential equations. The evaluation of the relations necessitates a linearization of the coupled differential equations (3.11). Furthermore, it is usefully to express the energy density e(~r ,t ) by a time dependent heat density:
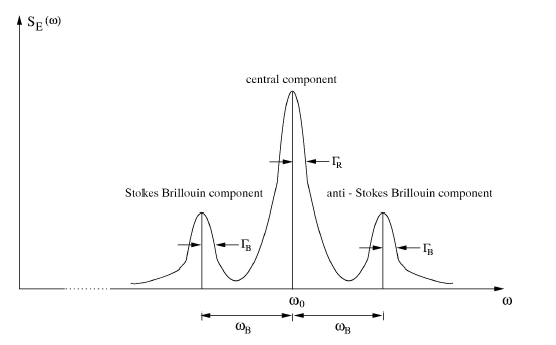
The above relations include the complete information about the scattering spectrum of a simple liquid, which can be written as:
The frequency dependence in that equation is that of a Lorentz function:
Another important expression for the evaluation of DLS data is given by the Einstein-Stokes relation, which relates the diffusion coefficient D, the shear viscosity ηs and to the radius r of a particle:
holds for simple fluids. In the case of multi-component critical systems the diffusion has to be considered within the framework of the mode-coupling theory. Mode-coupling theory yields a similar expression for the critical part of mutual diffusion coefficient:
with the correlation length ξ. More detailed descriptions of the mutual diffusion coefficient and its corrections within the scope of dynamic scaling and crossover theory will be presented in 2005-(II)-Critical Contribution, Dynamic Scaling and Crossover Theory.