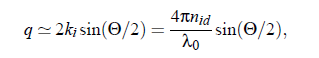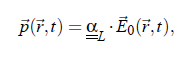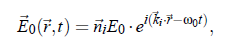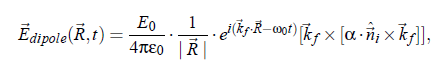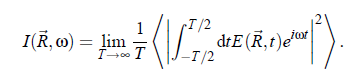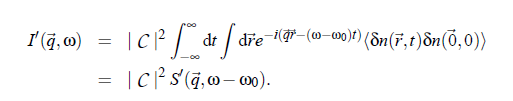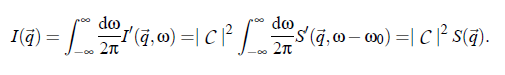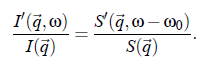2004-(II)-Dynamic light scattering
Article Index
In the last decades, light scattering techniques have been used with increasing effort for investigations of the physical properties of pure fluids and multicomponent fluids. The dynamic light scattering is a very powerful technique to determine the size of particles or to study critical fluctuations in multi-component fluids. According to the semi-classical theory, when light interacts with matter, the electric field of the light induces an oscillating electronic polarization in the molecules or atoms. With the aid of electromagnetic theory, statistical mechanics and hydrodynamics it is possible to gain information about the structural and dynamic properties of a sample.

Electromagnetic scattering theory:
Note:(Many calculation steps are skipped. Also many constants listed in the text are vectors. It's all about the red thread here.)
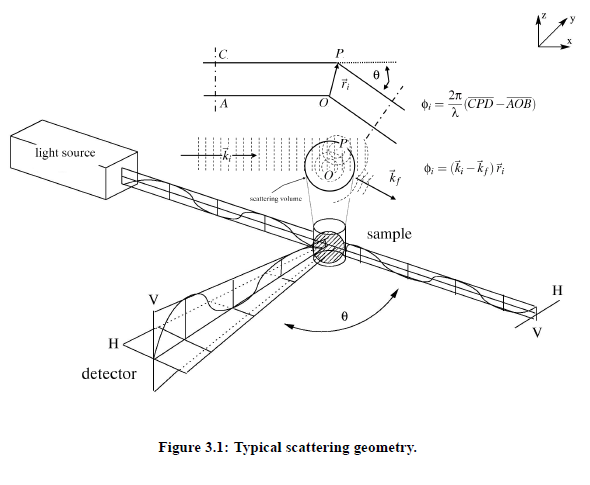
In the following, the underlying theory of dynamic light scattering on fluids is briefly summarized. A typical scattering geometry for light scattering experiments is shown in Fig.(3.1).
In principle, it is possible to vary the polarization of the incident light. However, with the help of scattering vector q~ follows from geometrical considerations, Fig.(3.1), the relationship between the wave vector ki that points in the direction of the incident plane wave, and kf which points in the direction of the outgoing waves .The scattering vector is defined as q~ = k −k . The amount of q~ is given by:
With the refractive index nid of the fluid, the laser wavelength λ0 in vacuo, and the scattering angle Θ. For a general description of interactions between a light beam and molecules, it is appropriate to study the induced dipole moment of one molecule in an electrical field. The relation between the dipole moment p~ of a molecule and the field E at the position ~r at time t is given by:
where αL denotes the polarizability tensor. In light scattering experiments the incident electromagnetic wave may be written as:
index i stands for incident plane wave and index f stands for the outgoing waves (towards the detector). with the circular frequency ω and the normal vector n~ . The field of the electromagnetic wave induces an oscillating electronic polarization. Hence, the molecules behave as Hertzian dipoles and provide a secondary light source. From the Maxwell-equations follows the light wave propagation in a detector direction kf:
with the electric field constant ε , and with R being the position of the detector. This eqation describes the electric field propagating from an elementary dipole originating from a molecule. The electrical field from all molecules in the scattering volume follows as:
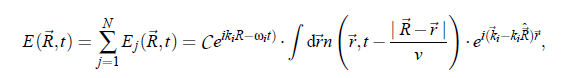
In principle, the relation describes the scattered light completely. In practice, however, the light intensity is obtained from the detectors. The intensity is defined as the ensemble mean:
or,
In this equation δn denotes the deviation of the local particle density from the average value ( δn := n(~r ,t ) − hni). I and S refer to the scattering volume where S (q~,ω −ω) is the so-called dynamic structure factor. In other words, S0 is the space and time Fourier transformed autocorrelation function of δn:
In conclusion, an important expression for the hydrodynamic considerations results:
- Prev
- Next >>