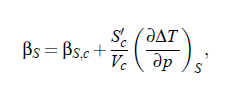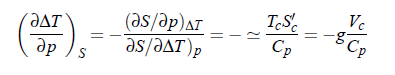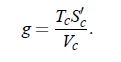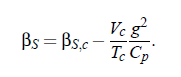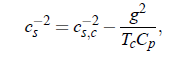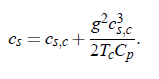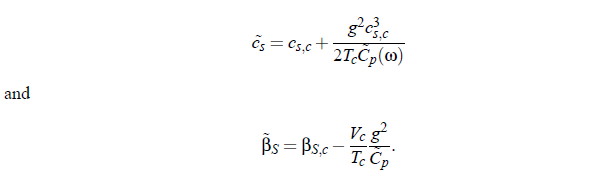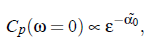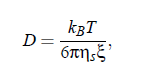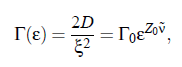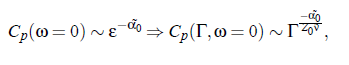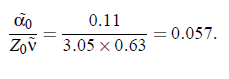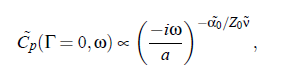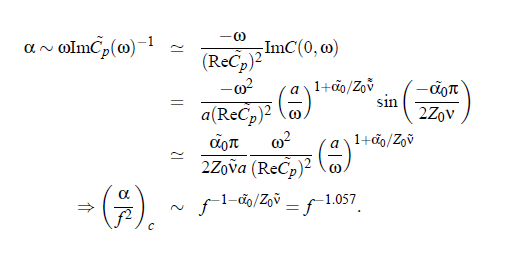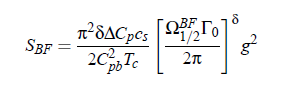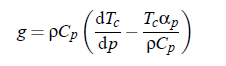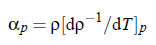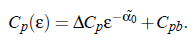2018-(I)-Critical Contribution, Dynamic Scaling and Crossover Theory
Article Index
The following project deals with the dynamic scaling aspects within the framework of Bhattacharjee-Ferrell theory. Furthermore, relationships between the critical sound attenuation and the dynamic scaling function are presented. Moreover, crossover effects for binary and ternary fluids are presented.
Bhattacharjee-Ferrell scaling hypothesis - binary systems:
Critical phenomena, as all continuous phase transitions, Show universal characteristics of their thermodynamic properties, if they belong to the same universality class and if their dimension is identical. The concepts and consequences of critical slowing down have been presented in 2005-(II)-Critical Phenomena and Universality. In particular, the light scattering is well represented and described by dynamic scaling theories, resulting from the mode-coupling considerations. However, the treatment of critical ultrasonic attenuation necessitates the development of new theories in order to get an access to critical fluctuations in a sound field. Bhattacharjee and Ferrell have presented a general theory of the critical ultrasonic attenuation, based on an extension of the concept of the frequency-dependent specific heat. This conception was firstly introduced by Herzfeld and Rice in 1928.
Critical sound attenuation:
For understanding the nature of critical sound attenuation, it is important to study the propagation velocity cs of low-frequency sound in the vicinity of the critical point. This kind of considerations allows to understand the coupling between the sound propagation and sound attenuation as well as the sound dispersion of sound velocity near the consolute point. The first thermodynamic studies of Bhattacharjee and Ferrell concentrated on the variation of volume V with pressure p , due to sound propagation at constant entropy S. As consequence of this examinations they got the isentropic compressibility βS at constant S :
where ∆T = T − T (p ) and index c denotes critical parameters. Moreover, the adiabatic temperature variation (∂∆T /∂p )S is expressed by:
roduces a dimensionless parameter g, which represents the system-specific coupling constant and describes the magnitude of coupling between critical density fluctuations and the propagating sound wave:
The sound velocity can be expressed as:
The next step in the procedure of Bhattacharjee and Ferrell considers the frequency ω for an applied pressure signal with its time dependence given by exp(−iωt ). Furthermore, with the aid of the frequency-dependent specific heat C (ω) it is possible to express the sound velocity cs and the compressibility βS as frequency dependent quantities (tilde denotes complex quantities, except for critical exponents ):
It is assumed that the critical part of the specific heat determines the complex sound velocity. Within the scope of dynamic scaling it is possible to write the dependence of C_p on the reduced temperature ε:
where α0 denotes the critical exponent. With the aid of the relationship of critical diffusion coefficient in that controls the relaxation of the concentration fluctuations and relates the diffusion coefficient D, to the viscosity ηs and the correlation length ξ of critical fluctuations:
(with the Boltzmanns’s constant kB , and absolute temperature T), it is possible to give an expression for the characteristic relaxation rate of a fluid:
where ν denotes the critical exponent of the correlation length and Z_0 denotes the dynamic critical exponent. The amplitude Γ_0 is a characteristic system-dependent constant. However, with regard to ultrasonic spectroscopy, it might be interesting to investigate the frequency dependence of the specific heat C_p; can express the temperature dependence in C_p in terms of the characteristic relaxation rate Γ:
where the value of the exponent is:
Consequently, one can get the frequency dependence of C_p at Γ = 0, by using the mode-coupling formalism. It follows:
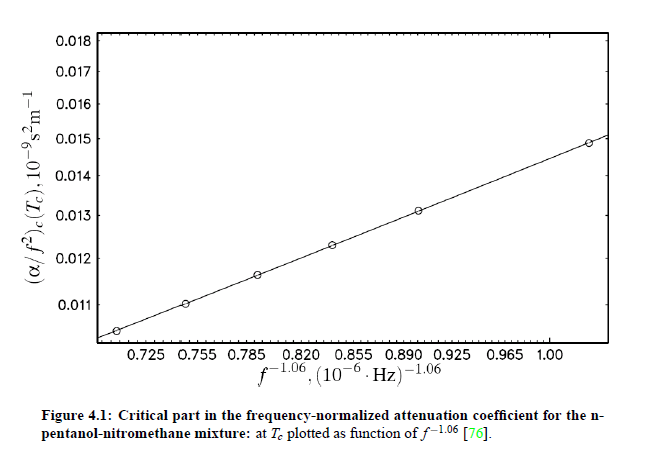
with a constant a. The attenuation coefficient α is proportional to:
The amplitude parameter A is related to the amplitude of the Bhattacharjee-Ferrell dynamic scaling model:
of the dynamic scaling model. Parameter g is the adiabatic coupling constan. According to the thermodynamic relation:
it can be obtained from the slope dT /d p in the pressure dependence of the critical temperature along the critical line and to the thermal expansion coefficient αp at constant pressure. The latter can be expressed with the aid of density ρ likewise at constant pressure:
∆C_p as well as C_pb are the amplitudes of the critical part and the background part, respectively, of the heat capacity at constant pressure:
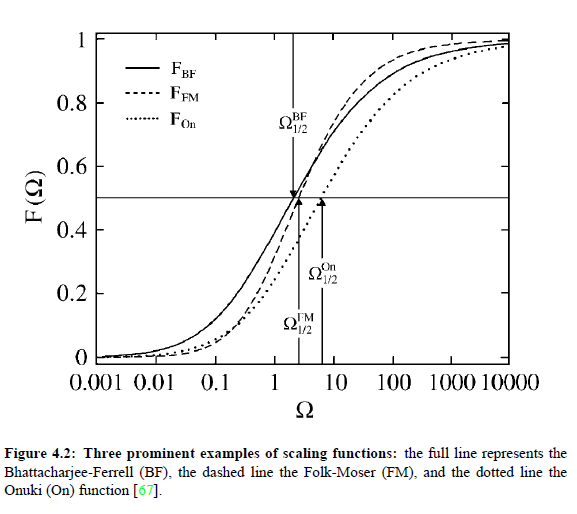
The function F_BF(Ω) is the so-called scaling function, which plays a central role it the Bhattacharjee-Ferrell theory. The properties of this special function will be treated with more details on the next side.
- Prev
- Next >>