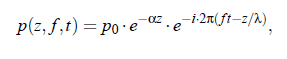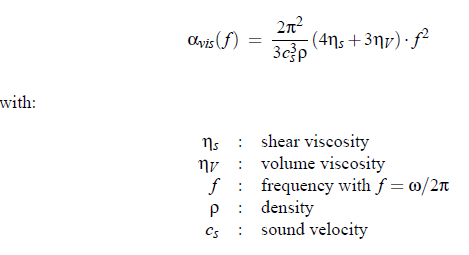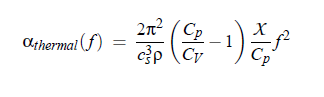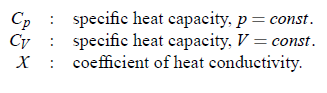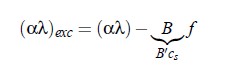2003-(II)-Ultrasonic techniques - The Resonator
Article Index
Ultrasonic technique is used to study fast elementary molecular processes in liquids. It is possible to study phenomena like stoichiometrically well defined chemical equilibria, including protolysis and hydrolysis reactions, conformational changes, association mechanisms and critical fluctuations. Oscillating compressions and decompressions in an ultrasonic wave cause oscillations of molecular arrangements in the liquid. An advantage of this technique is that the amplitudes of deformations in the ultrasonic waves are extremely small. It is a non-destructive technique. The available frequency range from 80 kHz to 5 GHz necessitates the use of different techniques: resonator methods and variable path length methods. However, this need provides another advantage of this methods. Because of different instrumental set-ups, systematic errors are unlikely to remain unnoticed.

Example of Ultrasonic Measurement Set-Up: "Resonator"
Classical absorption and background contribution:
Sound fields constitute temporal and spatial oscillations of the local pressure, which propagate through the liquid medium adiabatically, with its amplitude decreasing exponentially along the direction of propagation z by:
where α is the attenuation coefficient, cs is the sound velocity in the liquid for compressional waves of frequency f , cs = λ ·f , p is the sinusoidally oscillating sound pressure, p 0 = p (z = 0) and i2 = −1. The attenuation coefficient α is usually considered in ultrasonic spectroscopy. For our understanding of acoustical spectra, it is necessary to identify the physical mechanisms leading to sound attenuation in liquid systems. Oscillations of the liquid are coupled to the shear viscosity and other transport properties, which thus play an important role in compressional wave interactions. If the particle velocity is smaller than the sound velocity, the field in a viscous liquid is determined by the Navier-Stokes equations resulting in an acoustic absorption coefficient. An expression, which describes viscosity losses, is:
The relation (3.28) is strongly dependent upon the properties of the medium and on the frequency. Here the properties of a medium are mainly defined by the shear and the volume viscosity. Shear viscosity has the origin in Stokes friction. Additional losses result from the thermal conductivity, which has been fist shown in 1868 by Kirchhoff:
From history, it is a common practice to call the sum αvisc + αthermal as the ”classic” part of the acoustic attenuation coefficient αclass . In aqueous solutions the α_thermal contribution part to α_class is usually small (α_thermal α_vis ) and can be neglected. In principle the the shear viscosity ηs and the volume viscosity ηV in Eq.(3.28) are frequency dependent quantities. Therefore:
However, it is convenient for the discussion of measured acoustical spectra to assume the frequency-independent asymptotic ”background contribution” B , characterizing the total absorption at frequencies far above the experimental range. This includes the relaxation processes, occurring at frequencies well above the measuring range. Subtracting the asymptotic value from the measured absorption gives the so-called excess contribution (α/f 2 )exc and the excess absorption per wavelength (αλ)exc :
- Prev
- Next >>