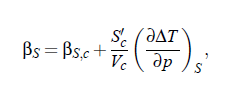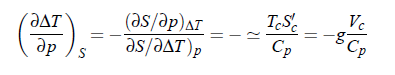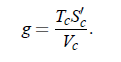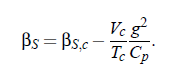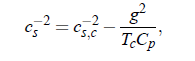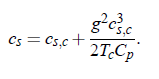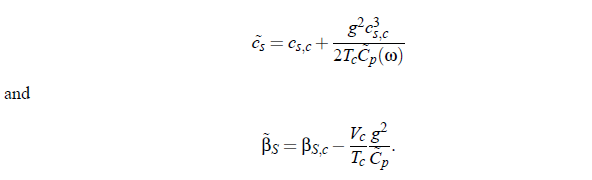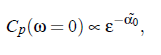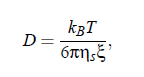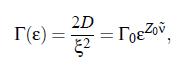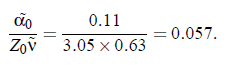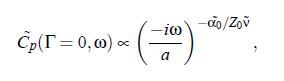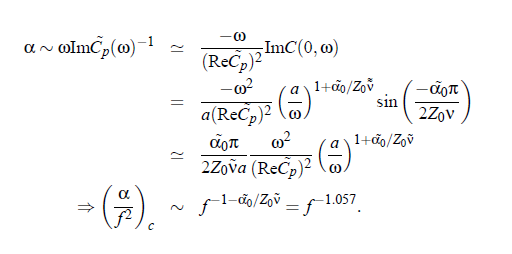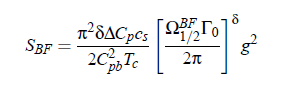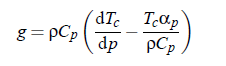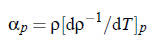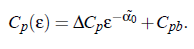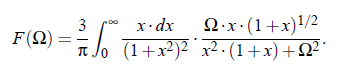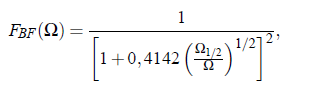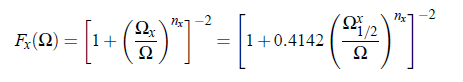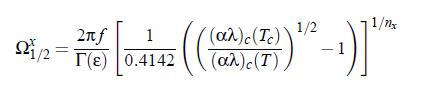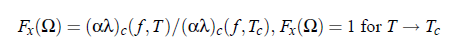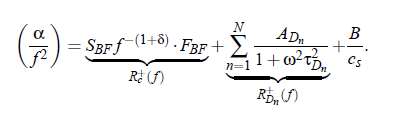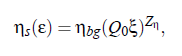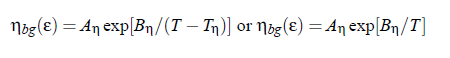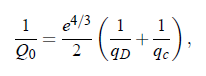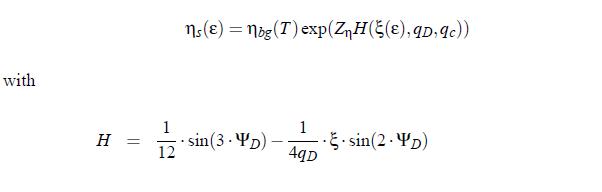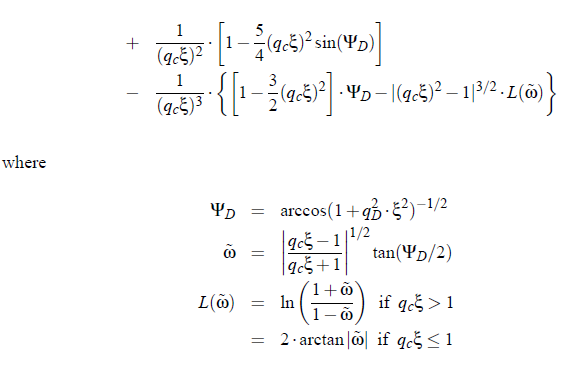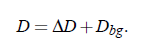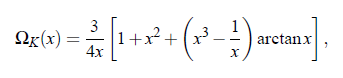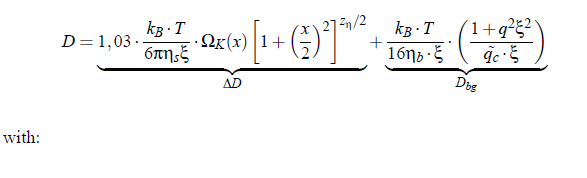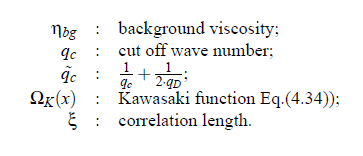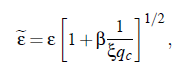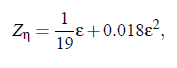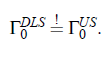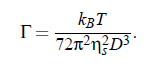2018-(I)-Critical Contribution, Dynamic Scaling and Crossover Theory
The following project deals with the dynamic scaling aspects within the framework of Bhattacharjee-Ferrell theory. Furthermore, relationships between the critical sound attenuation and the dynamic scaling function are presented. Moreover, crossover effects for binary and ternary fluids are presented.
Bhattacharjee-Ferrell scaling hypothesis - binary systems:
Critical phenomena, as all continuous phase transitions, Show universal characteristics of their thermodynamic properties, if they belong to the same universality class and if their dimension is identical. The concepts and consequences of critical slowing down have been presented in 2005-(II)-Critical Phenomena and Universality. In particular, the light scattering is well represented and described by dynamic scaling theories, resulting from the mode-coupling considerations. However, the treatment of critical ultrasonic attenuation necessitates the development of new theories in order to get an access to critical fluctuations in a sound field. Bhattacharjee and Ferrell have presented a general theory of the critical ultrasonic attenuation, based on an extension of the concept of the frequency-dependent specific heat. This conception was firstly introduced by Herzfeld and Rice in 1928.
Critical sound attenuation:
For understanding the nature of critical sound attenuation, it is important to study the propagation velocity cs of low-frequency sound in the vicinity of the critical point. This kind of considerations allows to understand the coupling between the sound propagation and sound attenuation as well as the sound dispersion of sound velocity near the consolute point. The first thermodynamic studies of Bhattacharjee and Ferrell concentrated on the variation of volume V with pressure p , due to sound propagation at constant entropy S. As consequence of this examinations they got the isentropic compressibility βS at constant S :
where ∆T = T − T (p ) and index c denotes critical parameters. Moreover, the adiabatic temperature variation (∂∆T /∂p )S is expressed by:
roduces a dimensionless parameter g, which represents the system-specific coupling constant and describes the magnitude of coupling between critical density fluctuations and the propagating sound wave:
The sound velocity can be expressed as:
The next step in the procedure of Bhattacharjee and Ferrell considers the frequency ω for an applied pressure signal with its time dependence given by exp(−iωt ). Furthermore, with the aid of the frequency-dependent specific heat C (ω) it is possible to express the sound velocity cs and the compressibility βS as frequency dependent quantities (tilde denotes complex quantities, except for critical exponents ):
It is assumed that the critical part of the specific heat determines the complex sound velocity. Within the scope of dynamic scaling it is possible to write the dependence of C_p on the reduced temperature ε:
where α0 denotes the critical exponent. With the aid of the relationship of critical diffusion coefficient in that controls the relaxation of the concentration fluctuations and relates the diffusion coefficient D, to the viscosity ηs and the correlation length ξ of critical fluctuations:
(with the Boltzmanns’s constant kB , and absolute temperature T), it is possible to give an expression for the characteristic relaxation rate of a fluid:
where ν denotes the critical exponent of the correlation length and Z_0 denotes the dynamic critical exponent. The amplitude Γ_0 is a characteristic system-dependent constant. However, with regard to ultrasonic spectroscopy, it might be interesting to investigate the frequency dependence of the specific heat C_p; can express the temperature dependence in C_p in terms of the characteristic relaxation rate Γ:
where the value of the exponent is:
Consequently, one can get the frequency dependence of C_p at Γ = 0, by using the mode-coupling formalism. It follows:
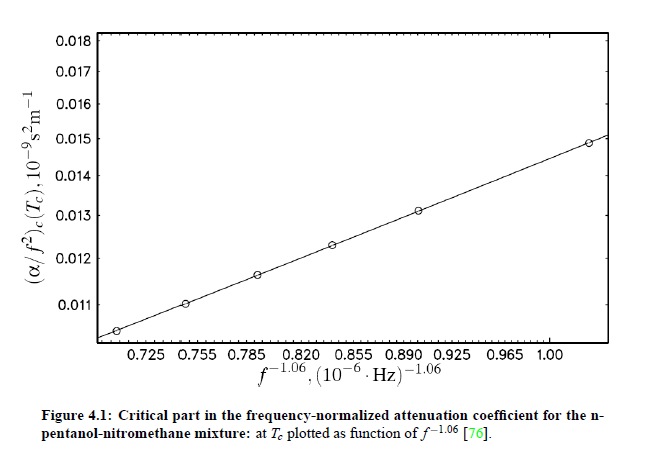
with a constant a. The attenuation coefficient α is proportional to:
The amplitude parameter A is related to the amplitude of the Bhattacharjee-Ferrell dynamic scaling model:
of the dynamic scaling model. Parameter g is the adiabatic coupling constan. According to the thermodynamic relation:
it can be obtained from the slope dT /d p in the pressure dependence of the critical temperature along the critical line and to the thermal expansion coefficient αp at constant pressure. The latter can be expressed with the aid of density ρ likewise at constant pressure:
∆C_p as well as C_pb are the amplitudes of the critical part and the background part, respectively, of the heat capacity at constant pressure:
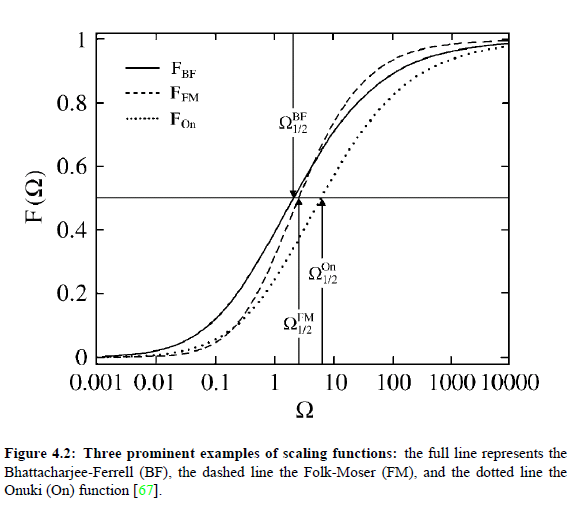
The function F_BF(Ω) is the so-called scaling function, which plays a central role it the Bhattacharjee-Ferrell theory. The properties of this special function will be treated with more details on the next side.
The scaling function F_x_BF(Ω):
Last decades, various theoretical expressions for the universal scaling function of ultrasonic attenuation spectra have been presented for critically demixing binary fluids. In Fig.(4.2) three prominent examples are shown:
In 1981 Bhattacharjee and Ferrell have presented the scaling function for sonic attenuation in analytical form:
Because of the difficulties to treat this integral, an empirical function has been developed:
with the half attenuation frequency Ω1/2 . The Folk-Moser (FM) scaling function FBF (Ω) as resulting from the renormalization group theory of the mode-coupling model and the function FOn (Ω), which Onuki (On) derived from an intuitive description of the bulk viscosity near a consolute point, are not available from theory in analytical form. Therefore, Behrends at al. developed a quasi-universal empirical form of scaling functions, in correspondence with the empirical function of
Bhattacharjee and Ferrell. These forms are shown in Fig.(4.2), and described by following relation:
where x denotes BF , FM and On, while Ωx and Ωx denote a characteristic frequency and the half-attenuation frequency of the scaling function, respectively. Finally, using the relation:
to evaluate experimental attenuation coefficient data along with relaxation rates Γ(ε) from light scattering and shear viscosity, it is possible to decide about the quality and validity of the scaling functions. The determination of the scaling function F(Ω) is usually based on the fact that A and cs are only weakly dependent upon temperature. Therefore, the scaling function can be derived as the ratio:
The measured total attenuation data contain contribution from critical fluctuation but also from noncritical processes. Assuming that all parts contribute to the ultrasonic attenuation spectrum additively, the ultrasonic spectra can be analytically represented as a sum of N Debye terms, the background contribution and the critical contribution: :
The Debye-terms can be likewise replaced by Hill-terms.
The crossover theory in binary mixtures (General conceptions of crossover theory):
The classical theories by van der Waals, Bertholt, and Dieterici describe pretty well the hydrodynamic and thermodynamic behavior of classical fluids in the mean-field region. Moreover, all their classical equations show the existence of a critical point. Unfortunately, they do not predict the non-analytic behavior in real systems. This fluid domain has been treated by Wilson, Fisher and Wagner within the framework of the renormalization-group theory. The conceptions and formalisms of this theory lead to a description in terms of scaling laws near the consolute point. Furthermore, renormalization-group theory has been quite successful in calculations and predictions of critical exponents. However, due to crossover effects this theory has a limited range of validity.
Unfortunately, the theoretical descriptions are valid only in a range extremely close to the critical point when ε → 0. There is no conception of extrapolation from the mean-field to the critical region. This so-called crossover-range has been reated 1986 in a paper by Albright at al, consistent with the renormalization-group theory. Their crossover descriptions for properties of fluids take into account, that besides the contributions from critical fluctuations to the critical behavior, there are further degrees of freedom, such as changes of molecular conformations and of the extent of hydrogen bonding. These kinds of effects do not couple to the critical fluctuations. Therefore, it is adequate to divide the modes of the considered liquid system into those that show only short range order and high frequency fluctuations and are only weakly coupled and into such which show long range fluctuations and are coupled strongly. These last ones lead to non-analytic behavior near the consolute point. Consequently, the existence of a cut-off Λ in the wave numbers of fluctuations, has to be taken into account when fluctuation dominated behavior of the system is studied. This view has been successfully applied to the van der Waals gas.
The Crossover corrections:
In the case of the dynamic light scattering, the shear viscosity as well as ultrasonic attenuation spectroscopy crossover corrections have to be taken into account when T is not sufficiently close to T. It has been shown, that close to the critical
point, in the asymptotic limit, the shear viscosity can be described by the expression:
here Q0 denotes the system-dependent critical amplitude and ξ the fluctuation correlation length. The background viscosity ηbg is given by the relation:
with the system specific parameters A_η , B_η, and T_η and with the absolute temperature T. The inverse critical amplitude of the viscosity Q−1, can be written as:
where qc and qD are the noncritical cut-off wave numbers. Eq.(4.28) is correct only in a region close to the critical point. Therefore, when treating data over a large temperature range, it is essential to consider the crossover corrections as has been presented by Burstyn at al. In that paper Burstyn et al. introduce a crossover function H (ξ,q_c ,q_D,), which is also dependent on the noncritical cut-off wave numbers q_c ,q_D as well as the correlation length ξ:
For large ε, the crossover function behaves as H (ξ(ε),q_D,q_c) → 0, so that η → ηbg. In the asymptotic limit the equation simplifies to the power law in. The influence of the crossover function is not only restricted to the shear viscosity. The cut-off wave numbers qc and qD play also an important role in the mutual diffusion coefficient, which is given by:
The value ∆D represents the singular contribution, which is shaped by the Kawasaki function ΩK:
with x = qξ. The mutual diffusion is then represented by:
Another important consequence resulting from crossover corrections is the significant influence of the values ξ0 and qc on the reduced temperature ε. Bhattacharjee and Ferrell have presented a correction expression that is based on the use of an effective reduced e temperature ε, which is given by:
with the parameter β = 1.18.
The crossover theory in ternary mixtures:
The crossover theory has been developed for binary mixtures. It is not self-evident that this theory is also valid for ternary mixtures. Moreover, the renormalization group ε-expansion predicts a dependence of the critical exponent of viscosity Zη upon the dimension of the considered system.
with ε (note, in this case ε is not the reduced temperature), the critical dimension dc = 4, and ε = dc −d , where d is the dimension of the system. Consequently, the value ε/19 for a 3d-Ising system, in first order for Zη . Taking into account the second order corrections, Zη = 0.065 results. This value has been predicted by the mode-coupling theory. In the case of tricritical point the critical dimension is reduced to dc = 3, as has been given by Pfeuty. As a consequence, ε = 0 and therefore Zη=0. It seems that there is no critical divergence of the viscosity. However, the ternary system, that has been investigated it this work is of type 2a and belongs to the same universality class for dynamical properties as the binary fluids. Thus, there is no reason to treat the experimental data different from the binary mixtures. Furthermore, it can be expected, that the crossover corrections are likewise valid.
Strategies of verifying the scaling function:
The formalism for the verification of the critical parameters and the scaling function calls for a specific treatment of experimental data within the framework of crossover formalisms as well as the Bhattacharjee-Ferrell theory of critical sound attenuation, Fig.(5.1). In principle, the scaling function can be derived directly from the ultrasonic measurements, by taking into account the Bhattacharjee-Ferrell theory. However, due to effects of critical slowing near T_c as well as the enormously increasing attenuation coefficient toward low frequencies, only the high frequency part of the critical contribution to the ultrasonic spectra is obtainable from attenuation coefficient measurements.Therefore Γ_US is only inaccurately known from acoustical spectrometry. For this reason and in order to reduce the number of unknown parameters in ultrasonic spectroscopy, the relaxation rate of order-parameter fluctuations has been additionally determined by shear viscosity and mutual diffusion coefficient measurements. Consequently, no distinction between the relaxation rate of critical fluctuations from ultrasonic measurements, Γ_US, and that from dynamic light scattering,Γ_DLS , will be made in the following:
This step is justified, because of the assumptions made by Bhattacharjee and Ferrell. According to their theory, local concentration fluctuations detected in the light scattering experiments are controlled by diffusion, of almost spherically shaped areas with concentration different from the mean. These fluctuating areas couple to the ultrasonic wave. Hence, the assumption for the characteristic relaxation rate Γ_DLS = Γ_US = Γ_0 can be done. In order to determine the characteristic relaxation rate Γ_0, dynamic light scattering and shear viscosity measurements have to be combined.
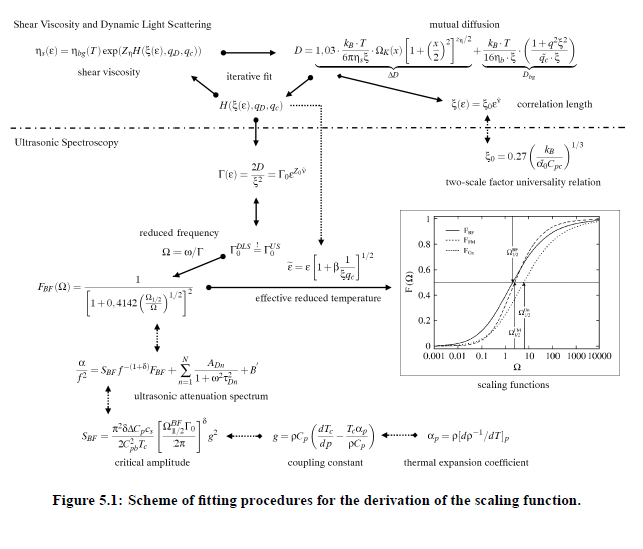
The Kawasaki-Ferrell relation can be rewritten to yield the relaxation rate of concentration fluctuations as a function of the diffusion coefficient and the shear viscosity:
The mutual diffusion coefficient as well as the fluctuation correlation length ξ can be derived from dynamic light scattering. However, crossover corrections have also to be taken into account. The crossover function H (ξ(ε),q_c ,q_D) contains an explicit dependence upon the fluctuation correlation length ξ and on the cut-off wave numbers qc and qD. Parameters ξ, qD and qc also control the mutual diffusion coefficient. Therefore, with the aid of an iterative fitting procedure the complicated expression of the crossover function H has to be applied simultaneously to the experimental shear viscosity and dynamic light scattering data. Finally,the value for Γ_0 determined in this way can be used to obtain the scaling function F (Ω). However, the critical amplitude is still an adjustable param eter. It weakly depends upon frequency due to the small critical exponent δ = α /(Z ν). If experimental heat capacity data are available, it is possible to calculate, with the amplitude SBF from thermodynamical quantities of critical mixture. Alternatively it is possible to extract the the amplitude from the ultrasonic spectra and to estimate the adiabatic coupling constant g. Furthermore, the amplitude of the correlation length ξ can be additionally verified with the help of heat capacity data using the so-called two-scale-factor universality relation:
with the heat critical exponent α0 = 0.11 and ∆ = 0.51 ± 0.03. However, as was mentioned in Section (4.4) the values for ξ0 and qc lead to noticeable changes of the reduced temperatures ε in the treatment of ultrasonic measurements. Hence, in the determination of the scaling function the reduced temperatures ε have to be corrected to get the effective reduced temperature ε . The fitting procedures applied on the basis of the dynamic scaling hypothesis and the crossover formalism are summarized schematically in Fig.(5.1).