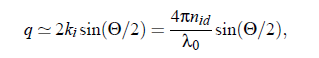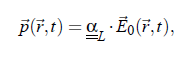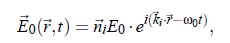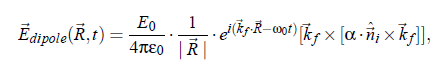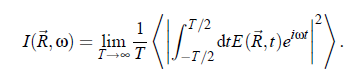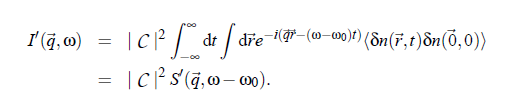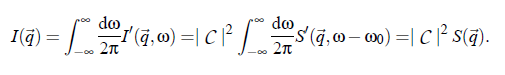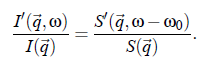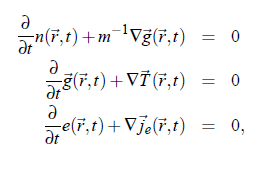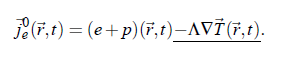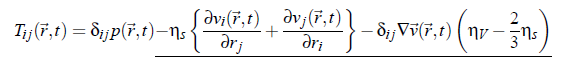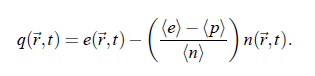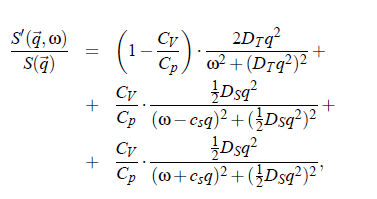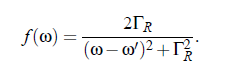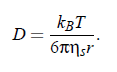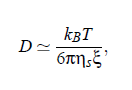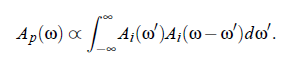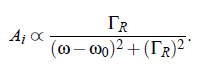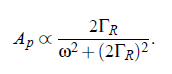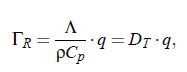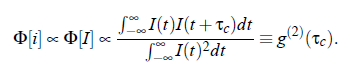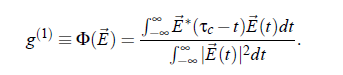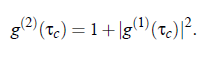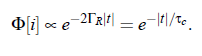2004-(II)-Dynamic light scattering
In the last decades, light scattering techniques have been used with increasing effort for investigations of the physical properties of pure fluids and multicomponent fluids. The dynamic light scattering is a very powerful technique to determine the size of particles or to study critical fluctuations in multi-component fluids. According to the semi-classical theory, when light interacts with matter, the electric field of the light induces an oscillating electronic polarization in the molecules or atoms. With the aid of electromagnetic theory, statistical mechanics and hydrodynamics it is possible to gain information about the structural and dynamic properties of a sample.

Electromagnetic scattering theory:
Note:(Many calculation steps are skipped. Also many constants listed in the text are vectors. It's all about the red thread here.)
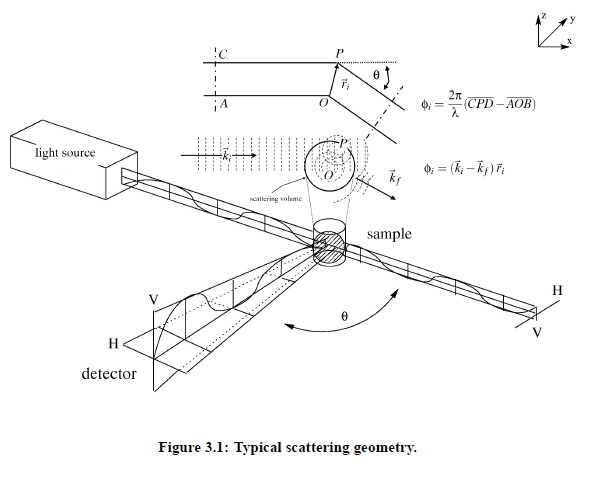
In the following, the underlying theory of dynamic light scattering on fluids is briefly summarized. A typical scattering geometry for light scattering experiments is shown in Fig.(3.1).
In principle, it is possible to vary the polarization of the incident light. However, with the help of scattering vector q~ follows from geometrical considerations, Fig.(3.1), the relationship between the wave vector ki that points in the direction of the incident plane wave, and kf which points in the direction of the outgoing waves .The scattering vector is defined as q~ = k −k . The amount of q~ is given by:
With the refractive index nid of the fluid, the laser wavelength λ0 in vacuo, and the scattering angle Θ. For a general description of interactions between a light beam and molecules, it is appropriate to study the induced dipole moment of one molecule in an electrical field. The relation between the dipole moment p~ of a molecule and the field E at the position ~r at time t is given by:
where αL denotes the polarizability tensor. In light scattering experiments the incident electromagnetic wave may be written as:
index i stands for incident plane wave and index f stands for the outgoing waves (towards the detector). with the circular frequency ω and the normal vector n~ . The field of the electromagnetic wave induces an oscillating electronic polarization. Hence, the molecules behave as Hertzian dipoles and provide a secondary light source. From the Maxwell-equations follows the light wave propagation in a detector direction kf:
with the electric field constant ε , and with R being the position of the detector. This eqation describes the electric field propagating from an elementary dipole originating from a molecule. The electrical field from all molecules in the scattering volume follows as:
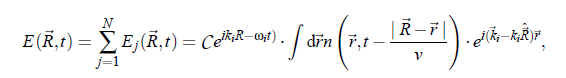
In principle, the relation describes the scattered light completely. In practice, however, the light intensity is obtained from the detectors. The intensity is defined as the ensemble mean:
or,
In this equation δn denotes the deviation of the local particle density from the average value ( δn := n(~r ,t ) − hni). I and S refer to the scattering volume where S (q~,ω −ω) is the so-called dynamic structure factor. In other words, S0 is the space and time Fourier transformed autocorrelation function of δn:
In conclusion, an important expression for the hydrodynamic considerations results:
Spectrum of scattered field - hydrodynamic considerations:
For the interpretation of the scattered spectrum of a fluid it is useful to consider the scattered field in terms of hydrodynamic approaches. In order to get access to hydrodynamics, the conservation and continuity equations have to be applied to a fluid volume element:
with the particle number density n(~r ,t ), the vector of momentum density g~(~r ,t ), the m mass, as well as the energy density e(~r ,t ). T (~r ,t ) is the stress tensor and j e (~r ,t ) the energy flux density. Finally, the expression of energy flux density is given by:
However, in the general case when the viscosity of fluid is not neglected, the expression of momentum density has to be completed to account for the volume viscosity ηV and the shear viscosity η. Consequently:
follows. In conclusion, with the aid of the equations of conservation and continuity a complete mathematical mean-field description of the hydrodynamics of a liquid results. The evaluation of the relations necessitates a linearization of the coupled differential equations. The evaluation of the relations necessitates a linearization of the coupled differential equations (3.11). Furthermore, it is usefully to express the energy density e(~r ,t ) by a time dependent heat density:
The above relations include the complete information about the scattering spectrum of a simple liquid, which can be written as:
The frequency dependence in that equation is that of a Lorentz function:
Another important expression for the evaluation of DLS data is given by the Einstein-Stokes relation, which relates the diffusion coefficient D, the shear viscosity ηs and to the radius r of a particle:
holds for simple fluids. In the case of multi-component critical systems the diffusion has to be considered within the framework of the mode-coupling theory. Mode-coupling theory yields a similar expression for the critical part of mutual diffusion coefficient:
with the correlation length ξ. More detailed descriptions of the mutual diffusion coefficient and its corrections within the scope of dynamic scaling and crossover theory will be presented in 2005-(II)-Critical Contribution, Dynamic Scaling and Crossover Theory.
Data evaluation of dynamic light scattering:
The central quantity of the evaluation of correlation spectroscopy is the decay time also named the correlation-time τ. Unfortunately, it is not possible to detect this frequency with classical optical methods. As a consequence, it is substantial to use optical mixing techniques, like homogenous mixing, heterogenous mixing (homodyne and heterodyne techniques) and the self-beating method.
Self-beating spectroscopy:
The principle of self-beating spectroscopy is based on mixing of scattered light with the original light on analyzing the resulting signal with low-frequency intermediate signal. This is realized in three steps:
Consider a signal of field strength E (R ,ω) with spectrum A , that has to be shifted into the lower frequencies. This happens with the aid of a local-oscillator signal. After this mixing procedure, it is possible to describe the scattered light with the help of convolution integral of the incoming spectrum (Ap , spectrum of the photon flux):
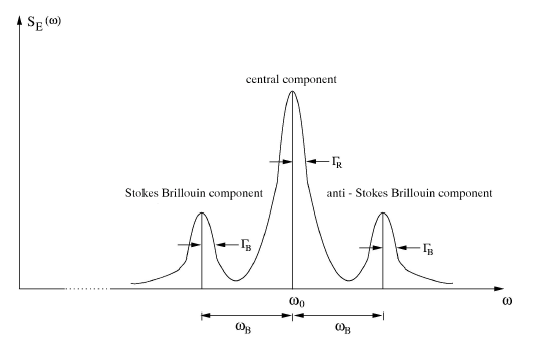
On the one side, the photon flux i(t ) is proportional to the light intensity, |I (ω)| = |E (ω)|^2 . On the other side, the considered Rayleigh line is of the shape of a Lorentz curve, with the the half-bandwidth ΓR and the center frequency ω_0:
For simple fluids the half-bandwidth ΓR (see Fig.(3.16)) of the Lorenz-curve can be represented by:
here denotes D_T the thermal diffusivity, Λ the thermal conductivity, ρ the density, C, the heat capacity at constant pressure p as well as q, the amount of the scattering vector. The next step is to find a tool to measure the spectrum. This can be realized with the aid of Correlation Spectroscopy.
Correlation Spectroscopy: The Wiener-Khinchin theorem |Af (ω)| = F Φ [f (t )] relates the signal f (t ) with the amount of the spectrum Af (ω). Here is F −1 the inverse Fouriertransform and Φ [f (t )] is the autocorrelation function of f(t). As mentioned before, the signal i(t) of the photon flux is proportional to the light intensity I (t). Practically, in an experiment the autocorrelation function Φ [i], which is proportional to the autocorrelation function of Φ [I ], is determined. Consequently, the following expression results:
In an experiment the interest is not focused on the intensity spectrum of the but in the spectrum of electric filed E (t ). Due to the well known relation I (t ) = |E (t )| , the expression (3.23) for the electric field is given by:
Finally, the autocorrelation function g (2) of the intensity I (t ) and the autocorrelation function g (1) of the field E (t) are related by the so-called Siegert relation:
In the DLS experiment one has to do with the Lorentz profile. The autocorrelation function of this profile is given by:
This equation allows to determine the half-with ΓR of Rayleigh-line from the correlation-time 1/2ΓR of the photon autocorrelation function.
Photon statistics: All considerations have been done with the assumption that i(t ) ∝ I (t ). In principle, this can be done for sufficiently high scattering count rates. For experiments with lower rates it is substantial to use adequate statistics.
Technical equipment:
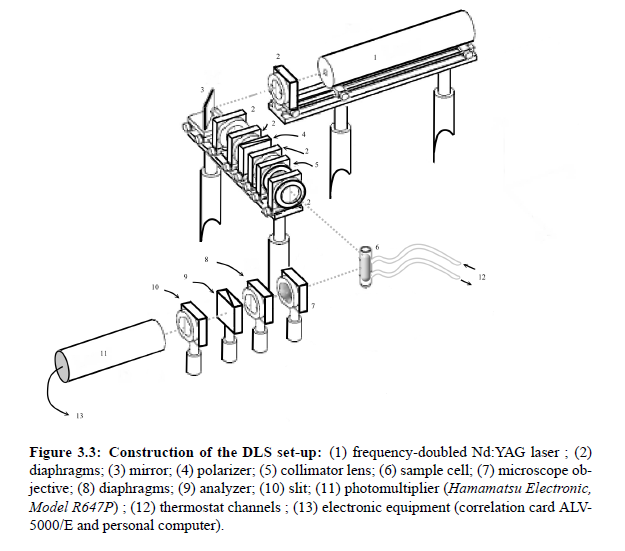
A typical dynamic light scattering set-up is presented in Fig.(3.3). A frequency-doubled Nd:YAG laser (1) is used as light source. The laser light passes several diaphragms (2), a polarizer (4) and a collimator lens (5) with focal length f = 100 mm and is then fed to the sample cell (6). The scattered light passes a microscope objective (7), a polarization analyzer (9) and the slit (10) with (d = 200 µm). Finally, the signal is detected by a photomultiplier (Hamamatsu Electronic, Model R647P) (12) that transforms a variation of intensity into a variation of voltage. The spectrometer is provided with a goniometer system which allow superior of scattering angle Θ. The received signal is analyzed with help of a correlation card ALV-5000/E with logarithmic timescale and with 288 channels. In principle it is possible to analyze the autocorrelation function in terms of a superposition of up to four exponentials and thus four correlation times τ . Hence the Rayleigh line
may be considered a sum of up to four Lorentz functions. Combining the correlation time τc with the Eqs.(3.1), (3.22) and (3.17) or (3.18), it is possible to determine the radius r of a particle and thus the correlation length ξ.