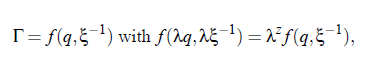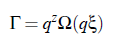2005-(II)-Critical Phenomena and Universality
Article Index
Dynamic scaling hypothesis and critical slowing down:
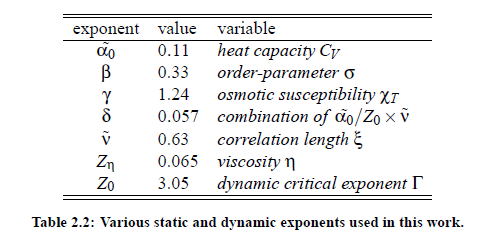
In different investigations it has been found that, close to the critical point, various properties of relevant systems follow power laws, so that their thermodynamic properties diverge or vanish at the critical point. According to the above connsiderations, the static scaling hypothesis takes into account the growing of characteristic length of a system near the critical point. However, another important observation is that all transport phenomena undergo a slowing down, caused by the increase of the correlation length ξ. Consequently,it can be assumed that, in addition to the characteristic length, there exists a characteristic time scale. The dynamic scaling hypothesis, which describes the phenomenon of so-called critical slowing down, was first introduced by Ferrell in 1967 and was subsequently generalized for magnetic systems by Halperin and Hohenberg (1969). The hypothesis implies that, when the temperature T of a system approaches the critical temperature T, the relaxation time τ is governed by ξ . Here v˜ is the exponent c ξ of the fluctuation correlation length, Table (2.2). With the life time of fluctuations, given by 1/τξ = Γ, and using generalized homogenous functions it is possible to to express Γ as a generalized homogenous function of the wave vector q and the reciprocal correlation length of the critical fluctuations ξ−1:
ere is z the degree of homogeneity. With the assumption λ = q−1 and the implementation of the relation Ω(qξ) = f (1, (qξ)−1) it is possible to scale the relaxation rate Γ:
The function Ω(qξ) is the so-called dynamic scaling function of the variables q and ξ. This function plays an important role in the treatment of critical dynamic phenomena. Within the scope of renormalization group theory of critical phenomena it is possible to calculate specific values of the critical exponents. The results of these calculations, which have been done by Gillou for static critical exponents and Burstyn and Sengers for dynamic critical exponents, are shown in Table (2.2). The development of dynamic scaling theories is a continuous process and undergoes permanent corrections and improvements
- << Prev
- Next