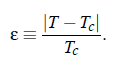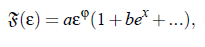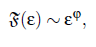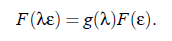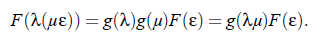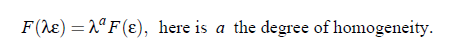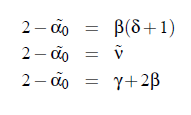2005-(II)-Critical Phenomena and Universality
Article Index
The fascination about critical phenomena is based on the universality of the behaviour of systems, which can be quite different in many of their properties. Theoretical models of critical behavior are based on the terms renormalization and scaling. Such a new model shall be verified by comprehensive measurement of coupled parameters of critically segregating binary fluids. In addition, binary mixtures are to be investigated whose spectra reflect both universal and individual behaviour. Of particular interest is the coupling of critical dynamics to elementary chemical processes.
The similarity of different systems can be described by universal power laws which determine the thermodynamic and transport properties close to a critical point. In order to study the critical behavior in different systems it is convenient to use the so-called reduced temperature:
When the temperature T of a system is close to its critical temperature T , some relevant parameters F follow a power law:
with x > 0. At ε → 0, that is T → T , all terms except the 1 in the brackets disappear. Therefore, F satisfies the power law:
with ϕ, denoting the critical exponent for the particular variable F.
Static scaling hypothesis:
In the course of the last fifty years theoretical and experimental investigations have been done to develop and to proof the hypothesis of universality. In 1965 Widom postulated the so-called scaling hypothesis, which is based on the assumption, that the singularities of different thermodynamic quantities near the critical point are represented by their generalized homogenous functions. When F denotes the free energy and ε the reduced temperature, it follows:
It means, when the parameter λ scales the reduced temperature ε, than λ likewise scales the function of ε. Furthermore, if µ is an additional scaled variable of the function g, than:
Comparison of the factors of the function of F (ε) implies that the relation g (λ)g (µ) = g (λµ) is only valid when g follows a power law. Hence:
From such mathematical considerations follows that differentials as well as integrals of homogenous functions are again homogenous functions. Consequently, it can be assumed that all thermodynamical quantities, which are derived from the free energy F , can be represented by power laws. Furthermore, the static scaling hypothesis provides also relations between the critical exponents of different parameters (see Table (2.1), for the meaning of the symbols):
In 1971 the renormalization group method has been developed by Wilson [ 15] to calculate the critical exponents. This theory showed that the critical exponents depend only on the spacial dimensionality d and the number n of components of a system. Moreover, the essential message of those considerations was that phase transitions with the same dimensionality of the order parameter belong to the same universality class. Various critical exponents of systems and their order-parameter are represented in Table (2.1).
- Prev
- Next >>